4 dimensions on 3D plot with matplotlib.

As a part of my hyperparameters tuning during my last machine learning project I was changing 3 parameters and scoring my models with mean absolute error. The process yielded 4 values:

1. n_features - number of features
2. n_est - number of estimators
3. max_depth - maximum depth of ensemble regressors
4. mean absolute value - the scoring value of model trained with varying 3 above parameters.

Now it is time for question. 

How to plot such data?

Depending on type of plot it is possible to extend the dimensionality of 3d plot with the following (in case of scatter plot):

1. marker size
2. marker type
3. marker colour/transparency.

In the summary it is possible to end up with 6 dimensions. But it may cause problems with plot interpretation when both markers' type and size are varied. To be more precise it may be hard to compare the size of two different markers (e. g. a dot and a cross). 

Now I will return to the problem I faced. The data is available on GitHub. With the following code snippet you will receive simple 3d plot with no information about the scoring value. 

 import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams


rcParams["font.size"] = 15

dat = pd.read_json("4d_plot_data.json")

xs = dat["n_features"]
ys = dat["n_est"]
zs = dat["mae"]
cs = dat["max_depth"]

xs2 = xs.unique()
ys2 = ys.unique()

xx, yy = np.meshgrid(xs, ys)
xticks = [0.05] + list(np.linspace(0.2, 1, 5))

fig, ax = plt.subplots(figsize=(25, 15), subplot_kw={"projection": "3d"})
ax.scatter(xs, ys, cs,
           marker=".")
ax.scatter(1, 100, 3, marker="v", c="r", s=100)
ax.set(ylabel="n_estimators",
       xlabel="n_features",
       zlabel="max_depth",
       zticks=cs.unique(),
       zlim=(3, 6),
       xticks=xticks,
       )
ax.set_title("No 4-th dimension")

plt.tight_layout()
plt.show()

Below is the plot that will be generated after running the code.

Well, the plot is rather hardly telling anything. The red triangle shows default parameters case. Let's then add 4-th dimension (size of the markers). The plotting function should now look like:

fig, ax = plt.subplots(figsize=(25, 15), subplot_kw={"projection": "3d"})
ax.scatter(xs, ys, cs,
           s=zs*-5,
           marker=".")

A little explanation - the mean absolute value that I received from sklearn cross_val_score function is multiplied by -1 so that the more, the better. That is why in the above code snippet it is multiplied by -5. There is one problem with such solution. The "the more, the better" principle is now reversed, so now parameters of better performing machine learning models are shown as smaller points. Below is the plot:

As you can see the sizes do not differ so much. Let's change the 4th dimension from size to points transparency. Firstly, we should transform MAE (mean absolute error) so that its values will be from 0 to 1. The process is called normalisation. Then we generate colour array (red, green, blue, alpha) and plot.

 # normalisation
alpha = ((zs-zs.min())/(zs.max()-zs.min()))

# colour array
rgba_colors = np.zeros((zs.shape[0], 4))
rgba_colors[:, 2] = 1.0
rgba_colors[:, 3] = alpha

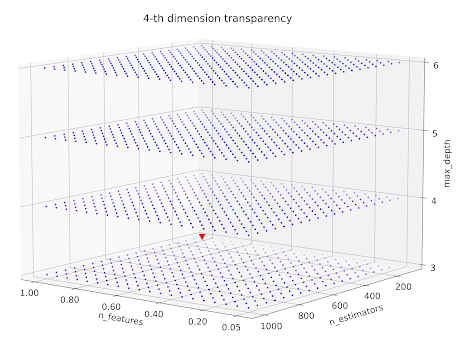
fig, ax = plt.subplots(figsize=(25, 15), subplot_kw={"projection": "3d"})
ax.scatter(xs, ys, cs,
           c=rgba_colors,
           marker=".")

With normalisation we keep the "the more, the better" principle. If we would like to plot alpha in the function of MAE we would do the following:

fig, ax = plt.subplots(figsize=(25,15))
ax.scatter(zs, alpha)
ax.set(xlabel="mean absolute error",
       ylabel="normalised")
plt.tight_layout()
plt.show()

And get such plot:

Below is our 4d plot.

It now looks better but not good enough to get some deep insight into MAE. Why don't we combine the power of transparency and size? 

 fig, ax = plt.subplots(figsize=(25, 15), subplot_kw={"projection": "3d"})
ax.scatter(xs, ys, cs,
           c=rgba_colors,
           s=alpha*100,
           marker=".")

Not bad, but still the least transparent points do not differ that much. What can we do? Let's embrace the power of power! Now we will change the linearity of the normalised mae to mae relationship. I chose the power of 5. Check the below code and plot:

rgba_colors[:, 3] = alpha**5
fig, ax = plt.subplots(figsize=(25, 15), subplot_kw={"projection": "3d"})
ax.scatter(xs, ys, cs,
           c=rgba_colors,
           s=alpha**5*100,
           marker=".")

Hey! I can now see where the biggest value of MAE is! 

But what happened? Check the plot below.

By raising normalised MAE to the power of 5 we "pushed down" the points close to the maximum. The point that had normalised MAE value of 1 remained there. We also lost most of the points that were closer to 0. But since we were interested in higher values the loss is acceptable.

Thanks for reading.